9. Functions and transformations

Our own functions

Once we start getting a complex sketch, there might be a lot of things going on in the body of the draw(). We can use comments to delineate things, but there's a better way: defining our own functions. Just like using variables with names to replace magic numbers, it helps us see what's going on if we package up a chunk of commands into a function. The following sketch illustrates this.

function setup() {
  createCanvas(400,400);
  smooth();
  frameRate(15);
  background(0);
}

function draw()
{
  fadeAway();          // move the execution to the function
  drawRandomEllipse(); // move the execution to the function
}

// Paint a transparent black rectangle over window
function fadeAway()
{
  fill(0,20);
  rect(0,0,width,height);
}

// Draw an ellipse of random color and size at random position
function drawRandomEllipse()
{
  fill(random(128,255),random(128,255),random(128,255));
  ellipse(random(width),random(height),100,100);
}

Defining our own function works much the same way as filling in setup() and draw(), but we choose our own name using the same rules as with variables. Now a glance at the draw() body makes very clear what's going on in each frame. Furthermore, we've now got a handy fadeAway() function that we can easily plug into other sketches.

Drawing a random ellipse is a pretty simple thing anyway, but imagine instead that we wanted to package up all the work of drawing some complex object, for example the L shape we drew last week. We could define a function drawL() function like this:

function drawL() {
  beginShape();
  vertex(50,50);
  vertex(50,150);
  vertex(150,150);
  vertex(150,100);
  vertex(100,100);
  vertex(100,50);
  endShape(CLOSE);
}

But we really want to be able to do is to put the shape in different places and at different sizes, as we can with ellipse(). We can do just that by defining our own function that takes parameters telling us where to draw it and how big to draw it.

function setup() {
  createCanvas(400,400);
  smooth();
  frameRate(15);
  background(0);
}

function draw()
{
  fadeAway();                // move the execution to the function
  drawRandomL();        // move the execution to the function
}

// Paint a transparent black rectangle over window
function fadeAway()
{
  fill(0,20);
  rect(0,0,width,height);
}

// draw random L shape
function drawRandomL()
{
  fill(random(128,255),random(128,255),random(128,255));
  drawL(random(width),random(height),random(50,150));
}

// Draw a L shape at the given position and of a given size
function drawL(x, y, s)
{
  beginShape();
  vertex(x,y);
  vertex(x,y+s);
  vertex(x+s,y+s);
  vertex(x+s,y+s/2);
  vertex(x+s/2,y+s/2);
  vertex(x+s/2,y);
  endShape(CLOSE);
}

Now we specify not just the name of our function, but also its parameters (names and types, like variable declarations). We can use the parameters within the body of the function, just like variables. We then call our function the same way we call built-in Processing functions. Details on function definition and parameters are in the Programming notes section.

In defining our drawL function, to draw the shape at a specified position, we simply use the variables x and y instead of 50 and 50 in the original sketch. To be able to draw in different sizes, we use the variable s instead of 100.

Shiffman, p. 109 (unfortunately not made into a downloadable example), shows a similar idea for drawing cars. One note is the use of a local variable named "offset". This variable is declared in the drawcar function, and therefore can only be used there. Local variables are a good way to temporarily keep track of something that will be used within the function, but nowhere else. (You can also use local variables in setup() and draw(); they're just functions with particular names.)

Another note is that Shiffman uses the function color() to package up red, green, and blue values into a single color value. This value is of a type called color (same name as the function). So instead of passing in three numbers, for red, green, and blue, he creates and passes a single color.

When we want to package up a calculation, rather than a set of drawing commands, we define a function that returns a value. For example, we could define a function that tells us whether or not the mouse is inside a rectangle, and use it in mouse-over and mouse press tests.

function draw()
{
  if(inRectangle(mouseX,mouseY,25,40,50,20))
    // Inside rectangle, so make it yellow
    fill(255,255,0);
  else
    // Outside rectangle, so make it green
    fill(0,255,0);
  rect(25,40,50,20);
}

// check if the (mx,my) is in the rect(x,y,w,h)
var inRectangle(mx, my, x, y, w, h) {
  return mx > x && mx < x+w && my > y && my < y+h;
}

Shiffman 7-4 shows how to package up a slightly more complicated calculation, to find the distance between two points. Note that he again uses some local variables inside his function to temporarily remember things while the function is being calculated.

Translation and scaling

So far, we've always treated the origin, (0,0), as the upper-left corner, with the x and y axes extending to the right and down, stepping one pixel at a time. In our drawL function above, we had to do some addition and multiplication for each vertex, to put it at the right place and at the right size. It would be more convenient to just tell Processing to move the origin and change the overall scale, so that we don't have to keep doing that ourselves.

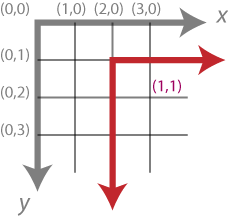
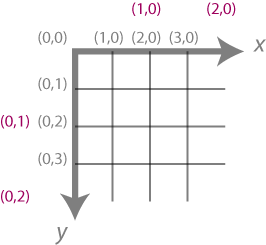
To do just that, Processing provides the functions translate() (given x and y offsets) and scale() (given x and y scaling factors). Give each of these operations a quick whirl, just plotting an ellipse before/after the operation.

We can use this technique to make the "drawL" function cleaner overall. Note that we only do translation since scaling would change the thickness of lines too and we do not want that for our general function. A problem arises in that the effects of these functions are cumulative, e.g., translate(10,5); translate(7,3); is the same as translate(17,8);. Thus if we aren't careful, we can lose our bearings. To help us out, Processing provides the push() function to store a copy the current coordinate system, and pop() function, to return back to it. We can push multiple coordinate systems, and they are treated in "last in first out" order, just like stacking plates on top of each other. Please note that Processing automatically reset transforms before calling draw().

function setup() {
  createCanvas(400,400);
  smooth();
  frameRate(15);
  background(0);
}

function draw()
{
  fadeAway();                // move the execution to the function
  drawRandomL();        // move the execution to the function
}

// Paint a transparent black rectangle over window
function fadeAway()
{
  fill(0,20);
  rect(0,0,width,height);
}

// draw random L shape
function drawRandomL()
{
  fill(random(128,255),random(128,255),random(128,255));
  drawL(random(width),random(height),random(50,150));
}

// Draw a L shape at the given position and of a given size
function drawL(x,y,s)
{
  push();
  translate(x,y);
  beginShape();
  vertex(0,0);
  vertex(0,s);
  vertex(s,s);
  vertex(s,s/2);
  vertex(s/2,s/2);
  vertex(s/2,0);
  endShape(CLOSE);
  pop();
}

Orientation

Going one step further, we can even reorient the coordinate system, so that the axes point diagonally across the window, for example. The function rotate() does that, given the angle to rotate (in radians).

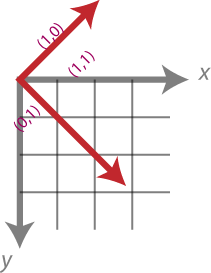
Give it a try, drawing a horizontal or vertical line before/after rotation. To rotate around some point other than the upper-left corner, we translate to that point first.

let a=0, da=0.05;    // drawing angle and increment

function setup()
{
  createCanvas(300,300);
  rectMode(CENTER);
  smooth();
}

function draw()
{
  background(0);
  translate(width/2,height/2);
  rotate(a);
  rect(0,0,200,10);
  a+=da;
}

A rotation transformation can be particularly useful when we want to have a sketch react not only to the position of the mouse, but also to the angle. We can use Processing's atan2() function to calculate the angle between a point and the origin. We provide as parameters the y and x coordinates, in that reversed order (recall from trig that the tangent is the opposite over the adjacent).

To compute an orientation with respect to some point other than the origin, we subtract out the coordinates of that point before calling atan2(), and then translate() to that point before calling rotate() with the computed angle.

function setup()
{
  createCanvas(300,300);
  smooth();
  stroke(255);
  strokeWeight(10);
}

function draw()
{
  background(0);
  let dx = mouseX - width/2;
  let dy = mouseY - height/2;
  let angle = atan2(dy, dx);  

  translate(width/2,height/2);
  rotate(angle);
  line(0,0,100,0);
}

Now for some freaky eyeballs, from the Processing example Basics | Math | Arctangent. It works exactly the same way, moving the center of the eyeball out along the x axis in the rotated coordinate system. Note the use of a function to package up the drawing of an eye, and the calling of this function with several different values for its parameters.

// Simplified from Processing Examples | Basics | Math | Arctangent

function setup()
{
  createCanvas(300, 300);
  smooth();
  noStroke();
}

function draw()
{
  background(50);

  drawEye( 50,  16,  80);
  drawEye(100,  85,  40);  
  drawEye( 90, 250, 160);
  drawEye(150,  80,  40); 
  drawEye(225, 160,  80);
}

// Draw an eye of size s at position (x,y)
function drawEye(x, y, s)
{
  // Make the eye look at the mouse
  var angle = atan2(mouseY-y, mouseX-x);
  push();
  translate(x, y);
  fill(255);
  ellipse(0, 0, s, s);
  rotate(angle);
  fill(153);
  ellipse(s/4, 0, s/2, s/2);
  pop();
}

Programming notes

Function definition

A function definition is of the form

type name(type1 paramName1, type2 paramName2, ...)
{
  statements
}

The name should follow the same rules and style as for variables (alphanumeric, beginning with a letter, internally capitalized, afunctioning Processing words). There need not be any parameters. The first type (the return type) can be "function", meaning that the function just executes statements and doesn't return any value.

Return

A function can return a value (e.g., like min()). The statement "return value;" stops the function right there, and returns the value to whoever called the function. A function that doesn't return a value can just call "return;" to stop right there.

Scope

We've seen several different variable scopes. Recall that global variables, declared before setup, can be used anywhere and hold their values across function calls. Local variables are declared within a function, are only available within the function, and are reinitialized each time. The same holds for function parameters. Note that we can reuse the same variable (or parameter) name in different functions -- they're totally separate.