Short Assignment 9 is due Wednesday.
Last time, we saw the Iterator interface. It has just three methods: hasNext, next, and remove. We use them as follows, where T denotes whatever type the iterator returns, i.e., whatever type is contained in the data structure we're iterating through, and ds is the data structure:
Iterator<T> iter = ds.iterator();
while (iter.hasNext()) {
T value = iter.next();
// Code that uses value goes here.
// Followed by an optional call:
iter.remove();
}We assume that the call ds.iterator() creates an object that implements the Iterator interface. That is, the iterator method runs the new operator somewhere along the line.
When we use an iterator in a linked list, we often want more functionality than the standard Iterator interface provides. In fact, Java supplies a standard ListIterator class. Its concept of "current" is different from the one we have seen. It has a "cursor position" between two elements in the list. A call to next returns the element after the cursor and moves the cursor forward. A call to previous returns the element before the cursor and moves the cursor backwards. Because of the way this works, alternating calls to next and previous will keep returning the same element. In addition to the methods in Iterator, the ListIterator interface requires the following methods:
previous: return the previous element in the list and move the cursor forward.hasPrevious: return a boolean indicating whether there is a previous element.add: add an element at the current position, just before the cursor (so that a call to previous would return that element and a call to next would be unaffected).set: replace the element last returned by next or previous.remove: in this interface, remove the element most recently last returned by a call to next or previous.nextIndex: return the index of the element that would be returned by a call to next.previousIndex: return the index of the element that would be returned by a call to previous.Calls to the remove and set methods are invalid if there has never been a call to next or previous or if remove or add has been called since the most recent call to next or previous.
The ArrayList class has a method that returns a ListIterator, also. There is a separate class LinkedList, which behaves like our circular doubly-linked list with a sentinel. Both implement the interface List, which requires a number of methods, including all that we saw for ArrayList plus Iterator and ListIterator. They differ in the amount of time operations take. For instance, a get, set, or add on a LinkedList requires time proportional to the distance that the index is from the nearest end of the list. Therefore, an add to either the front or end of a LinkedList takes constant time, unlike an ArrayList. If a ListIterator is used, the time required for any method in the interface is constant. For an ArrayList, the time for an add or remove is proportional to the number of elements after the element added or removed, even if using a ListIterator.
Because the conventions and operations are different from what we have implemented in SentinelDLL, we will show how to implement a ListIterator using this new concept of the current element. We extend the Iterator interface by declaring the CS10ListIterator interface in CS10ListIterator.java.
Because we have removed some of the methods from the SentinelDLL class, we need a new interface for the list class to implement. This new interface, CS10IteratedList in CS10IteratedList.java, is similar to the LinkedList interface in CS10LinkedList.java. The methods add, remove, get, next, and hasNext—all of which require access to the current instance variable—are gone.
There one new method: listIterator. This method will return an object that can iterate through the object whose class implements CS10ListIterator. This returned object starts an iteration.
SentinelDLLIterator classSentinelDLLIterator.java is a modified version of the circular, doubly linked list with a sentinel that includes an iterator. The first thing to notice is that the SentinelDLLIterator class implements the CS10IteratedList interface, and so the methods that were in LinkedList but not in CS10IteratedList are missing from SentinelDLLIterator.
The second thing to notice is that the SentinelDLLIterator class has just sentinel as an instance variable; there is no current instance variable, as there was in SentinelDLL.
But the most salient feature of our SentinelDLLIterator class implementation is the inner class DLLIterator, which implements the ListIterator interface. The DLLIterator class is private. Users of the SentinelDLLIterator can still get a DLLIterator by calling the listIterator method. Moreover, because DLLIterator implements the public CS10ListIterator interface, once any part of any program has a reference to a DLLIterator, it can call the public methods in CS10ListIterator on it. The constructor is private, however, so that the only way to create a DLLIterator object is to call the method listIterator on a SentinelDLLIterator object.
And, perhaps most importantly, by making DLLIterator an inner class of SentinelDLLIterator, the methods of DLLIterator can access anything that the methods of SentinelDLLIterator can access. That would include the instance variable sentinel, as well as anything that is public in the Element class (such as data, next, and previous).
The DLLIterator class has two instance variables:
current is chosen so that the implicit cursor is between current and current.next. This may seem a strange thing to do, but it allows us to go through a list, removing elements either forward or backward by alternately calling next and remove, or previous and remove.lastReturned is a reference to the Element whose data was returned by the most recent call to next or previous. This information is needed by remove and set. If next or previous was never called, or if a call to remove or add has changed the list since the last call to next or previous, this instance variable has the value null.From how we've defined current, it needs to be advanced in next before we return an object when moving forward and after determining the object to return when moving backward. In order for everything to work, current initially references the sentinel (rather than, say, sentinel.next).
I have included an equals method in DLLIterator, and it is set so that two DLLIterator objects are considered equal if they are currently referencing the same Element. The code checks to ensure that both objects involved are DLLIterator objects, and it returns false if they're not.
Returning to the SentinelDLLIterator class, there is a new method listIterator. It creates a new DLLIterator for the SentinelDLLIterator object and returns a reference to it. This listIterator method is made to be called from outside the SentinelDLLIterator class, and because it returns a reference to a DLLIterator, its return value may be assigned to CS10ListIterator or even Iterator (since ListIterator extends Iterator).
In the SentinelDLL class, the toString method now uses the iterator. Notice how toString uses the iteration paradigm from before, with a while-loop whose test includes the call iter.hasNext and whose body includes the call iter.next.
The DLLIterator created in toString is independent of any other DLLIterator in existence. Where one DLLIterator's current is has no effect at all on where another DLLIterator's current is.
We can really see this independence in ListTestIterator.java. Here, our test driver creates a DLLIterator by the line
CS10ListIterator<String> iter = theList.listIterator();The current instance variable of this DLLIterator is moved by next and previous and used by add. But when we call theList.toString, the DLLIterator created and used by toString does not affect the DLLIterator in main.
Similarly, the DLLIterator created and used in calls to addFirst and addLast are independent of all others. Therefore adding to the front or back of a list does not change the current element in iter.
I have also added a "clear" option that iterates through the list, removing all objects. (I could have used the clear method, but chose not to). I have added a "print reversed" option that runs through the list backwards, after advancing to the end.
The "nested print" option really shows the power of separate iterators. Here, we have two DLLIterators, outer and inner. For each list object traversed by outer, we perform a full traversal of the list with inner. This task would be impossible if we were limited only to the methods we had in our original linked list implementations.
Having multiple iterators on the same object can be very useful, as we just saw. As long as none of them modifies the list everything is fine. Problems may arise, however, if any of the iterators modifies the list. In particular, if one iterator removes an element that is the current element of another iterator, things can get very messy. Even changing the list by using addFirst and addLast can change how things work, and calling clear is definitely a problem!
Multiple threads (streams of control) can really cause problems. Suppose that you are on the second to last element in the list, you call hasNext and true is returned, and then call next. Should be safe, right? Well, not if somebody else in another thread removed the last element between the two calls. (Maybe somebody clicked on a button or a Timer went off between the calls, and the method registered with the listener changed the list.)
Because of this potential, a bulletproof iterator should throw an exception if the list has been modified in any way except via the iterator's own operations. We won't worry about these situations for now.
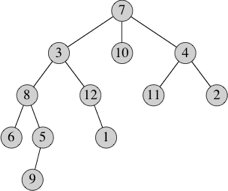
We use rooted trees to represent hierarchical relations. Here is an example of a rooted tree:

A tree is built up from nodes. The node at the top of the tree is the root; in our example, the root is node 7. Each node has zero or more children, which are also nodes. For example, node 4 has two children, which are nodes 11 and 2. An edge connects a node with its child, for example the edge (4, 11). Nodes with no children are external nodes or leaves (such as nodes 9 and 10), and nodes with at least one child are called internal nodes (such as node 4). A child has exactly one parent (except for the root, which has no parent); for example, the parent of node 11 is node 4. Nodes with the same parent are siblings, such as nodes 11 and 2. A path in a tree is a sequence of unique nodes such that each node in the sequence has an edge to the nodes before and after it. In our example, one path consists of nodes 6, 8, 3, 7, 4. If there is a path from the root to node y such that node x appears on the path, then node x is an ancestor of node y, and node y is a descendant of node x. For example, node 3 is an ancestor of node 5, and node 5 is a descendant of node 3. A subtree rooted at a node consists of all descendents of that node, including the node itself. The subtree rooted at node 3 comprises nodes 3, 8, 6, 5, 9, 12, and 1.
Here are some examples of relations that can be represented by trees:
Object.The book gives additional examples. We will see more examples as the course progresses.
The examples above have some cases where the order of children does not matter (the Java inheritance hierarchy, file systems, and organization charts). For an HTML document, however, the order does matter. In representing trees we end up imposing an order on children, whether it is important or arbitrary.
We will not use the tree code from our textbook, but feel free to read it. The book uses a different approach from what we have seen so far. We built our linked lists from Element objects, where Element is an inner class. We access the elements directly from within SentinelDLL or SLL and access fields with code such as current.next. We provide no access to Element objects from outside of the class, however. Instead, we have a current instance variable built into the class, or we provide an iterator. Java does the same thing.
In the textbook, they build up their lists, trees, graphs, etc. from Position objects. Position is an interface (in Position.java) with a single method: element. This method returns the data stored in the object. Their node classes for lists, trees, etc. implement the Position interface. They then let the user get a reference to one of these nodes via methods such asroot in the Tree interface. Although root actually returns a reference to a Node object, its return type is Position.
Therefore, you can do only two things with a Position:
element on it to get the data saved within it.LinkedBinaryTree, which deal with positions. These methods will cast the Position to the correct type (after verifying that it is the correct type) and use it.We call Position an opaque type. You can pass it around and use it to mark where you are in a data structure, but you're not permitted to access anything within it. From a software engineering point of view, this is the way to go. On the other hand, this approach complicates the tree code and hides its basic simplicity. Therefore, we have implemented our own tree code. We do not implement code for general trees (although we could do so), concentrating instead on the common special case of binary trees.
A binary tree is a rooted tree in which each node has zero, one, or two children. We designate each child as either a left child or a right child, even when it's an only child. Here are two different binary trees:
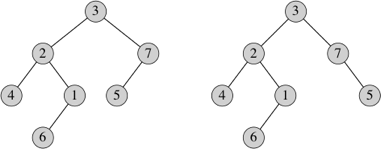
They differ only in that node 5 is a left child in the tree on the left, and it's a right child in the tree on the right.
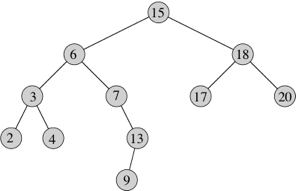
Binary trees come up in a multitude of applications: decision trees, expression trees, code trees (such as in Huffman encoding, which you'll be doing in Lab Assignment 2), and binary search trees. We'll see binary search trees later in the course, but the idea is that we store a value in each node, called the key, such that for every node x, the keys in its left subtree (the subtree rooted at its left child) are less than or equal to the key in node x, and the keys in its right subtree (the subtree rooted at its right child) are greater than or equal to the key in node x. Here is a binary search tree, with keys appearing inside the nodes:
Rather than having an inner class to represent the nodes and manipulating them via an outer class (as we did for linked lists), this time we make the tree nodes themselves more powerful and manipulate them from other classes. This code is in BinaryTree.java. The class BinaryTree has three instance variables:
left is a reference to the left child.right is a reference to the right child.data is the data stored in the node.The values of left or right are null if these children are absent. The book also keeps a reference to the parent node, which can be useful for certain applications.
We access a binary tree through its root node. If we want to access a subtree, we access it through the root of the subtree. Thus, some of the methods in the BinaryTree class pertain to individual nodes, but we can always consider a node to be the root of a subtree.
BinaryTree classHere are the methods in the BinaryTree class. Although they are called on a BinaryTree object, many of them actually pertain to just the node at the root of a subtree, and that's what they're called on.
left and right to null.isInternal returns a boolean indicating whether the node is an internal node.isLeaf returns a boolean indicating whether the node is a leaf.hasLeft and hasRight return booleans indicating whether the node has left and right children, respectively.getLeft and getRight are getter methods for the left and right children.setLeft and setRight are setter methods for the left and right children.getValue and setValue are getter and setter methods for the data in the node.size returns the number of nodes in the subtree rooted at the node, including the node itself.height gives the height of the node, which is the number of edges in a longest path from the node down to a leaf. For example, in the binary trees above, the node with key 2 has height 2, and the node with key 4 has height 0.equals method determines whether two subtrees have exactly the same structure and the same data.fringe returns an ArrayList containing the data in all the leaves of the subtree rooted at the node, from left to right across the leaves. It calls the private helper method addToFringe. For the binary trees above, fringe would return an ArrayList with the values 4, 6, 5.toString returns a String that indents two spaces for each increase in the depth of a node: the number of edges in the path up to the root. If you turn your head sideways and look at the string returned by toString, you can see the structure of the binary tree. toString calls the private helper method toStringHelper.preorder, inorder, and postorder return lists (using the Java interface List) containing the data in the nodes of the subtree rooted at the node, according to the three types of traversal orders that we'll see later in the course.reconstructTree creates a binary tree, based on the results of preorder and inorder traversals of the tree. We'll see how this method works later in the course.You might have noticed that although the BinaryTree class includes a height method, it does not include a depth method. Think about why there is not enough information in a BinaryTree object, as defined, to write a depth method.
Notice that several of the methods are recursive. For example, the size method. That's because we can characterize the size of a subtree recursively:
The size of a subtree is 1 (for the root of the subtree), plus the size of its left subtree, plus the size of its right subtree. The size of an empty subtree is 0.
The size and height methods use a special ternary operator ? : in Java. (Ternary means that it takes three operands.) The first operand, appearing before the question mark, is a boolean expression. If the boolean expression evaluates to true, then the value of the operator is the second expression, between the question mark and the colon. Otherwise, the value of the operator is the third expression, which follows the colon. In the expression hasLeft() ? left.size() : 0 in the size method, if the call hasLeft() returns true, the expression's value is the value returned by calling left.size(). Otherwise, hasLeft() returns false, and the expression's value is 0.
Similarly, we can characterize the height of a node recursively:
The height of a leaf is 0. The height of an internal node is 1 plus the maximum heights of its children.
You might recall that the equals method must take a reference to Object as its parameter, no matter what class it appears in. Therefore, the first thing that equals does is make sure that other references a BinaryTree object. Generic types in Java are designed strangely, and although you would think that the first line should be
if (other instanceof BinaryTree<E>) {we have to put a question mark between the angle brackets instead. (I don't fully understand why, but it shows how difficult it is to design a programming language that is both easy to use and internally consistent.) After the instanceof check, we then cast other to a reference to BinaryTree<E>, this time using <E> and not <?>. The line @SuppressWarnings("unchecked") is another strange thing in Java; we could omit the line, but we'd get an annoying warning. Once we have cast the parameter, we have a complicated expression that checks for five requirements being met:
other does.other does.other are equal, according to the equals method on the generic type E.Notice how we rely on the || operator short-circuiting in the latter two tests. If hasLeft returns false, then do not call left.equals to check the left subtree, and ditto for the right subtree.
In the toStringHelper method, what's passed in is a string containing some number of spaces. These spaces precede each node in the subtree rooted at this. Each recursive call to toStringHelper increases the number of spaces by two. Although we usually think of processing the left subtree before the right subtree, in toStringHelper, we do the opposite so that when you look at the output with your head tipped to the left it looks like the structure of the binary tree. The toString method just gets things started off with an empty string.
We could have written the toStringHelper method in one line, using the ternary operator:
return (hasRight() ? right.toStringHelper(indent + " ") : "")
+ (indent + data + "\n")
+ (hasLeft() ? left.toStringHelper(indent + " ") : "");In the fringe method, we create an empty ArrayList and pass it to addToFringe. This ArrayList has data added to it if the node is a leaf, and it's passed to the left and right subtrees otherwise. We could have done something like we did for toString, but that would require appending two ArrayList objects.
The BinaryTree class has a main method as a driver. It starts by creating as tree this tree:
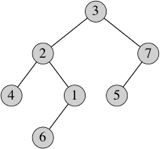
Then it exercises the size, height, and fringe methods. Next, it traverses the tree using preorder, inorder, and postorder traversals (again, we'll see what these are later on). With the preorder and inorder traversals, it creates a copy of the tree in tree1 and exercises equals method, which returns true. After making a change to the data in the right child of the root of tree1, it runs the equals method again, this time getting back false. Finally, it makes another copy of tree in tree2, changes the left child of the root in tree2 to have no left child, and runs the equals method again, once again getting back false.