Last time, we saw how to query a binary search tree and how to insert into one. We started looking at how to remove a node from a binary search tree. Let's restart our look at removing a node.
The overall strategy for removing a node z from a binary search tree has three basic cases but, as we shall see, one of the cases is a bit tricky.
z has no children, then we simply remove it by modifying its parent to replace z with the sentinel as its child.z has just one child, then we elevate that child to take z's position in the tree by modifying z's parent to replace z by z's child.z has two children, then we find z's successor y—which must be in z's right subtree—and have y take z's position in the tree. The rest of z's original right subtree becomes y's new right subtree, and z's left subtree becomes y's new left subtree. This case is the tricky one because, as we shall see, it matters whether y is z's right child.A word about the case in which z has two children. Many books, including our textbook and the first two editions of Introduction to Algorithms, treated this case differently and, at first blush, more simply. Instead of moving z's successor into z's position in the binary search tree, they took the information in z's successor (here, the key and value instance variables), copied them into z, and then removed this successor. Because z's successor cannot have two children (think about why), removing it will fall into one of the first two cases.
That approach turns out to be quite a bit simpler than what we're going to do. So why are we adding all the extra complexity? Because the code that uses the binary search tree might keep references to nodes within the tree. If the code to remove a node changes what's in a node, and if it removes a different node than the one requested, all heck can break loose in the rest of the program. So, instead, we will guarantee that if you ask to remove node z, then it is node z and only node z that is actually removed, and all references to all other nodes remain valid.
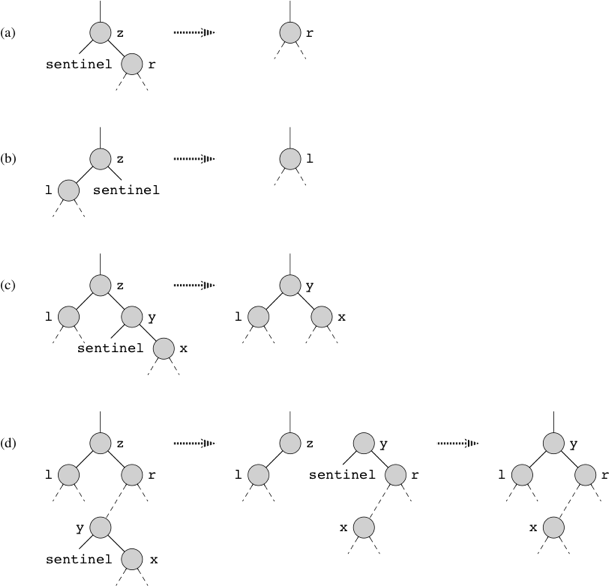
The code for removing a given node z from a binary search tree organizes its cases a bit differently from the three cases outlined previously by considering the four cases shown here:

If z has no left child (part (a) of the figure), then we replace z by its right child r, which may or may not be the sentinel. When z's right child is the sentinel, this case deals with the situation in which z has no children. When z's right child is not the sentinel, this case handles the situation in which z has just one child, which is its right child.
If z has just one child, which is its left child l (part (b) of the figure), then we replace z by its left child.
Otherwise, z has both a left child l and a right child r. We find z's successor y, which lies in z's right subtree and has no left child but could have a right child x. We want to splice y out of its current location and have it replace z in the tree.
If y is z's right child (part (c)), then we replace z by y, leaving y's right child x alone.
Otherwise, y lies within z's right subtree but is not z's right child (part (d)). In this case, we first replace y by its own right child x, and then we replace z by y.
In order to move subtrees around within the binary search tree, we use a helper method, transplant, which replaces one subtree as a child of its parent with another subtree. When transplant replaces the subtree rooted at node u with the subtree rooted at node v, node u's parent becomes node v's parent, and u's parent ends up having v as its appropriate child.
protected void transplant(Node u, Node v) {
if (u.parent == sentinel) // was u the root?
root = v; // if so, now v is the root
else if (u == u.parent.left) // otherwise adjust the child of u's parent
u.parent.left = v;
else
u.parent.right = v;
if (v != sentinel) // if v wasn't the sentinel ...
v.parent = u.parent; // ... update its parent
}This method is protected because subclasses might need to call it, but code using the BST class should not need to know about it.
The first two lines handle the case in which u is the root. Otherwise, u is either a left child or a right child of its parent. Yhe last two cases of the if-ladder take care of updating u.parent.left if u is a left child or u.parent.right if u is a right child. We allow v to be the sentinel, and the last two lines update v.parent if v is not the sentinel. Note that transplant does not attempt to update v.left and v.right; doing so, or not doing so, is the responsibility of transplant's caller.
With the transplant method in hand, here is the method that removes node z from a binary search tree:
public void remove(Node z) {
if (z.left == sentinel) // no left child?
transplant(z, z.right); // then just replace z by its right child
else if (z.right == sentinel) // no right child?
transplant(z, z.left); // then just replace z by its left child
else {
// Node z has two children.
Node y = minimum(z.right); // y is in z's right subtree, and y has no left
// child
// Splice y out of its current location, and have it replace z in the BST.
if (y.parent != z) {
// If y is not z's right child, replace y as a child of its parent by
// y's right child and turn z's right child into y's right child.
transplant(y, y.right);
y.right = z.right;
y.right.parent = y;
}
// Regardless of whether we found that y was z's right child, replace z as
// a child of its parent by y and replace y's left child by z's left
// child.
transplant(z, y);
y.left = z.left;
y.left.parent = y;
}
}The remove method executes the four cases as follows. The first two lines handle the case in which node z has no left child, and the next two handle the case in which z has a left child but no right child.
The remainder of the method deals with the remaining two cases, in which z has two children. We first find node y, which is the successor of z. Because z has a nonempty right subtree, its successor must be the node in that subtree with the smallest key; hence the call to minimum(z.right). As we noted before, y has no left child. We want to splice y out of its current location, and it should replace z in the tree. If y is z's right child, then the last three lines replace z as a child of its parent by y and replace y's left child by z's left child. If y is not z's right child, the lines
// Splice y out of its current location, and have it replace z in the BST.
if (y.parent != z) {
// If y is not z's right child, replace y as a child of its parent by
// y's right child and turn z's right child into y's right child.
transplant(y, y.right);
y.right = z.right;
y.right.parent = y;
}replace y as a child of its parent by y's right child and turn z's right child r into y's right child, and then the last three replace z as a child of its parent by y and replace y's left child by z's left child.
Each line of remove, including the calls to transplant, takes constant time, except for the call to minimum. Thus, remove runs in O(h) time on a tree of height h.
BST classThe code in BSTTest.java tests the BST class. We have not discussed the toString method, but it is similar enough to how the toString method in BinaryTree.java operates that you should be able to figure out how it works.
When we visit the nodes in a rooted tree, we are traversing the tree. Of the many possible orders for visiting nodes, three are most common. We think of them recursively, in terms of when to visit a node and when to visit its subtrees. We'll show examples in terms of this binary search tree, where we imagine visiting a node as printing out its key:
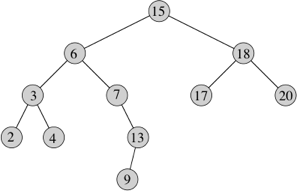
Going back to our binary tree (not binary search tree) code in BinaryTree.java, we see methods preorder, inorder, and postorder. Each appends data from a subtree to a List. But List is an interface, and in the driver, you can see that it's actually implemented by a Java LinkedList. Here's the preorder method:
public void preorder(List<E> dataList) {
dataList.add(data);
if (this.hasLeft())
left.preorder(dataList); // recurse on left child
if (this.hasRight())
right.preorder(dataList); // recurse on right child
}The other two methods just move the call to add to different locations in the code:
public void inorder(List<E> dataList) {
if (this.hasLeft())
left.inorder(dataList); // recurse on left child
dataList.add(data);
if (this.hasRight())
right.inorder(dataList); // recurse on right child
}
public void postorder(List<E> dataList) {
if (this.hasLeft())
left.postorder(dataList); // recurse on left child
if (this.hasRight())
right.postorder(dataList); // recurse on right child
dataList.add(data);
}Traversing rooted trees comes up quite often. For example, the TreeSet implementation of the Set interface stores information in a binary search tree, and the iterator returned by its iterator method is guaranteed to iterate over the set elements in increasing order. Not surprisingly, this iterator traverses the binary search tree using an inorder traversal.
There's another interesting use of traversals in binary trees. If all keys are distinct and you have both a preorder and an inorder traversal, you can reconstruct the entire binary tree. The method reconstructTree in the BinaryTree class does so. How does this method work? The first node in a preorder traversal is the root. The root is somewhere in the middle of an inorder traversal, with everything in its left subtree before it and everything in its right subtree after it. In the preorder traversal, all of the nodes in the left subtree are visited before anything in the right subtree. So we can build the tree recursively as follows:
leftPre in the code) and one list from the inorder traversal (leftIn in the code). Do so by iterating through the preorder and inorder lists until getting to the root in the inorder list.leftPre and leftIn lists, use them to recursively build the left subtree.rightPre in the code) and one list from the inorder traversal (rightIn in the code). Do so by iterating through the remainder of the preorder and inorder lists, starting from where we left off in step 1 and jumping over the root in the inorder list.rightPre and rightIn lists, use them to recursively build the right subtree.How long does it take to traverse a rooted tree with n nodes? The answer is Θ(n) time. Here's an easy way to see it. We have to consider each edge twice. The first time is when we traverse the edge from the parent down to a child. The second time is when we traverse the edge from the child back to the parent. Conceptually, there is also an edge down into the root, representing the work performed in the initial call of the method. How many edges are there? It is a fact that in any tree—whether or not we think of it as a rooted tree—the number of edges is n − 1. Add in one more for the edge down to the root, and conceptually, there are n edges, each traversed twice. That makes the total time Θ(n).
We can think of expressions as being represented by trees. To keep things simple so that we don't have to think about operator precedence, let's consider only fully parenthesized expressions. Take the expression ((17.5 + (5.0 / x)) * (y - 4.0)). We can represent it by this binary tree:
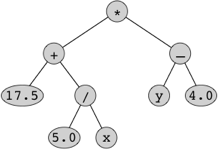
Although we could build an expression tree on top of the binary tree code, we will write a new set of classes to represent expression trees. Each node will be its own type, so that we'll have nodes for variables, constants, and each of the binary operators. We won't include unary operators (such as unary minus) or ternary operators (such as the ? : operator of Java), but we could—and we could not include unary operators if all expression trees had to be binary trees.
The code for expression trees is in this zip file. (I will show you individual classes, but this is the easy way to download the whole thing.) First, look at Expression.java. It is an interface that says that an Expression must provide two methods: eval and deriv. The eval method evaluates an expression and returns its value in a double. The deriv method gives returns an expression that is the symbolic version of the derivative with respect to a particular variable. An Expression should also override toString.
Next, look at Constant.java. To use a constant, you call its define method, just giving a double with the value of the constant. The define method is static and calls the constructor, which is private, so that the only way to define a constant is by calling define. The constructor just saves the value of the constant in the instance variable myValue, and then the define method returns a reference to the Constant object. Because Constant implements Expression, anywhere you have declared a reference to an Expression, the reference may actually be to a Constant. The eval method just returns the value in myValue, and the deriv method always returns a constant whose value is 0.0, since the derivative of a constant with respect to any variable is 0. The toString method just returns the String representation of myValue.
This scheme, where the constructor is private and there is a static method that calls the constructor is a variant of a design pattern called the factory pattern. Instead of constructing objects directly, users of the class have to go through a method to create an object. One use is to allow the factory to decide to create a subclass object when asked to create a superclass object. Another is to give the user options on what parameters to pass to create the object. For example, complex numbers can be represented using polar or rectangular coordinates. Either way you present two double values, and so you cannot overload the constructor to accept either representation. You can create two factories, however, one of which expects polar coordinates and the other of which expects rectangular coordinates. For example:
class Complex {
public static Complex fromCartesian(double real, double imag) {
return new Complex(real, imag);
}
public static Complex fromPolar(double mag, double phase) {
return new Complex(mag * cos(phase), mag * sin(phase));
}
private Complex(double a, double b) {
// Code to store into private instance variables goes here.
}
}
Complex c = Complex.fromPolar(1, pi);It is less clear why we would want to use this pattern in the Constant class,, but it will become clearer later.
The Variable class in Variable.java class is similar, but it has a symbol table to save variable values. These are saved in a Map that is implemented using a HashMap. Again, there's a define method, but this time it is overloaded. The two-parameter form takes the name of a variable as a String and a value for the variable, storing the name and value in the symbol table. The one-parameter form takes just the name of the variable, and it stores the name in the symbol table with null for the value. A variable whose value is null is defined but uninitialized. The constructor, called by both define methods, stores the variable's name in the instance variable myName. There is an assign method that stores the value in the symbol table entry for the variable. The eval method looks up the variable in the symbol table, using myName as the key, and it returns the value found in the symbol table for the key given by myName. The deriv method determines whether the variable v given as the parameter matches myName. If it does, then the derivative is 1; otherwise, the derivative is 0. The correct Constant is defined and returned in either case. The toString method just returns myName.
Some errors can occur when using variables, and instead of just printing error messages, we throw exceptions. We have exceptions for three types of errors:
define method throws a MultiplyDefinedVariableException, defined in MultiplyDefinedVariableException.java.define method, the assign method throws an UndefinedVariableException, defined in UndefinedVariableException.java.eval method throws an UnassignedVariableException, defined in UnassignedVariableException.java.The classes in Sum.java, Difference.java, Product.java, and Quotient.java all perform eval by evaluating their operands and performing an operation on them. The only difference is the operator. Therefore, we have an abstract class in BinaryOp.java that has the template for evaluating a binary expression and another template for toString. These templates call abstract functions doOperation and getOperation, repectively. (The latter returns a String representation of the operator). It also has accessor methods to get the first or second expression.
Notice that evaluating an expression is really a postorder traversal of the expression tree. To evaluate a BinaryOp, first evaluate its two subtrees, and then apply the appropriate binary operator to the results of evaluating the subtrees.
Let's look at the Sum class more carefully. It provides the necessary two methods, which are fairly trivial. It supplies its deriv method, which adds the derivatives of its operands. But the interesting thing is Sum.make. Here we see the power of a factory method. It tries to simplify the expression. If the two expressions it is adding are constants, it adds them to get a new constant. If either operand is 0 it returns the other. So in three of the four cases it does not even create a Sum object! The other three operations are similar in how they try to simplify the resulting expression in their make methods.
Finally, look at the driver in ExpressionDriver.java. After the main method, we have several static wrapper methods. They alleviate the need to call the static methods in the above classes with the name of the class. We also use method names plus, minus, times, and over instead of the class names Sum, Difference, Product, and Quotient. In that way, we can construct the expression tree above using lines of code such as
Variable xVar = define("x", 2.0);
Variable yVar = define("y", 6.0);
Expression first = plus(constant(17.5), over(constant(5.0), xVar));
Expression second = minus(yVar, constant(4.0));
Expression third = times(first, second);Or we can replace the last three lines by
Expression fourth = times(plus(constant(17.5), over(constant(5.0), xVar)),
minus(yVar, constant(4.0)));The driver also verifies that the three exceptions work correctly.