Lecture 22, May 19

Code discussed in lecture

• BST.java
• RBTree.java
• RBTreeTest.java

Red-black trees

Red-black trees are a variation of binary search trees. In fact, we'll create a class RBTree as a subclass of BST, but I had to make several changes to the version of the BST.java file we saw previously. In particular, I made many of the methods that had been in the BST class taking a Node as a parameter be in the Node class instead. Why? Because that way, I get dynamic binding when I make a Node subclass within RBTree.

Red-black trees are balanced binary trees: the height of an n-node red-black tree is always O(lg n). The binary-search-tree operations on a red-black tree take O(lg n) time in the worst case.

Definition of a red-black tree

A red-black tree is a binary search tree with one extra bit per node: a color, which is either red or black. As in our binary search tree, absent nodes are represented by the sentinel.

In a red-black tree, we think of the leaves as the sentinel, and the sentinel is always black. All instance variables of binary search trees and their nodes are inherited by red-black trees (key, value, left, right, parent, sentinel, and root ). We don't care about the key in the sentinel, but we do care about its color and structural instance variables (left, right, and parent).

A red-black tree obeys the five red-black properties:

1. Every node is either red or black.
2. The root is black.
3. Every leaf (the sentinel) is black.
4. If a node is red, then both its children are black. (Hence there can be no two red nodes in a row on a simple path from the root to a leaf.)
5. For each node, all paths from the node to descendant leaves contain the same number of black nodes.

The height of a node is the number of edges in a longest path to a leaf. The black-height of node x, which we write as bh(x), is the number of black nodes (including the sentinel) on the path from x to a leaf, not counting x. By property 5, black-height is well defined. Here is a red-black tree with keys inside nodes and with node heights h and black-heights bh labeled:

By property 2, any node with height h has black-height at least h/2. (At most half the nodes on a path to a leaf are red, and so at least half are black.)

We can also show that the subtree rooted at any node x contains at least 2^bh(x) − 1 internal nodes. The proof is by induction on the height of x. The basis is when h(x) = 0, which means that x is a leaf, and so bh(x) = 0. The subtree rooted at x has 0 internal nodes, and 2⁰ − 1 = 0. Any child of x has height h − 1 and black-height either b (if the child is red) or b − 1 (if the child is black). By the inductive hypothesis, each child has at least 2^{bh(x) − 1} − 1 internal nodes. Thus, the subtree rooted at x contains at least 2 ⋅ (2^{bh(x) − 1} − 1) + 1 = 2^bh(x) − 1 internal nodes. (The  + 1 is for x itself.)

These two facts lead to the following theorem:

A red-black tree with n internal nodes has height at most 2 lg (n + 1).

To prove the theorem, let h and b be the height and black-height of the root, respectively. By the above two facts, n ≥ 2^b − 1 ≥ 2^h/2 − 1. Adding 1 to both sides and then taking logs gives lg (n + 1) ≥ h/2, which implies that h ≤ 2 lg (n + 1).

Operations on red-black trees

The non-modifying operations on binary search trees—minimum, maximum, predecessor, successor, and search—are unchanged for red-black trees.

Inserting and remove are not so easy.

If we insert, what color to make the new node?

• Red? Might violate property 4.
• Black? Might violate property 5.

If we remove a node, what color was the node that was removed?

• Red? OK, since we won't have changed any black-heights, nor will we have created two red nodes in a row. Also, cannot cause a violation of property 2, since if the removed node was red, it could not have been the root.
• Black? Could cause there to be two reds in a row (violating property 4), and can also cause a violation of property 5. Could also cause a violation of property 2, if the removed node was the root and its child—which becomes the new root—was red.

Rotations

You might recall the rotation operation from the midterm exam. It's the basic tree-restructuring operation. We need rotations to maintain red-black trees as balanced binary search trees. A rotation changes only structural instance variables and maintains the binary-search-tree property.

We have both left rotation and right rotation operations. They are inverses of each other. A rotation is called on a node within a binary search tree.

Here is what rotations do:

Look at the method leftRotate in RBTree.java. It assumes that this.right is not the sentinel and that the root's parent is the sentinel. The code for rightRotate is symmetric to leftRotate.

Here's an example of a call to leftRotate:

Notice that before rotation, the keys in x's left subtree are less than x's key of 11, and the keys in x's right subtree are greater than x's key. The left rotation makes y's left subtree into x's right subtree. After rotation the keys in x's left subtree are still less than x's key, which is less than the keys in x's right subtree, which is less than y's key of 18, which is less than the keys in y's right subtree.

Each rotation operation takes O(1) time, since only a constant number of instance variables are modified.

Inserting into a red-black tree

To insert into a red-black tree, we start by calling the insert method from the superclass BST. We then make a new node have the sentinel as its children, and we color the new node red. (The getNewNode method is new here and in BST.java. It's how we ensure that the new node created is from the correct Node class.)

Then, the insert method calls rbInsertFixup because we might have violated a red-black property. Which properties might be violated?

1. OK
2. If z is the root, then there's a violation. Otherwise, OK.
3. OK.
4. If z.parent is red, then there's a violation: both z and z.parent are red.
5. OK.

The rbInsertFixup method maintains the following loop invariant:

At the start of each iteration of the while-loop:

1. z is red.
2. There is at most one red-black violation:

• Property 2: z is a red root, or
• Property 4: z and z.parent are both red.

We've already seen that the loop invariant holds initially.

When the loop terminates, it's because z.parent is black. So property 4 is OK. Only property 2 might be violated, and the last line fixes it.

Showing that the loop invariant is maintained is a bit tricky. There are six cases, three of which are symmetric to the other three. The cases are not mutually exclusive. Let's consider just the cases in which z.parent is a left child. Let y be z's uncle (that is, y is z.parent's sibling).

• Case 1: y is red

  
  
  
  • z.parent.parent (z's grandparent) must be black, since z and z.parent are both red and there are no other violations of property 4.
  • Make z.parent and y black, so that now z and z.parent are not both red. But property 5 might be violated.
  • Make z.parent.parent red to restore property 5.
  • The next iteration has z.parent.parent as the new z (i.e., z moves up two levels).

• Case 2: y is black, and z is a right child.

  
  
  
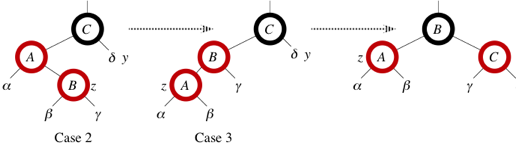
  • Left rotate around z.parent, so that now z is a left child, and both z and z.parent are red.
  • Takes us immediately to case 3.

• Case 3: y is black, and z is a left child.

  • Make z.parent black and z.parent.parent red.
  • Then right rotate on z.parent.parent.
  • We no longer have two red nodes in a row.
  • z.parent is now black, and so the loop test fails and the loop terminates.

Analysis

It takes O(lg n) time to get throught the insert call up to the call of rbInsertFixup. Within rbInsertFixup:

• Each iteration takes O(1) time.
• Each iteration is either the last one or it moves z up two levels.
• Since there are O(lg n) levels, it takes O(lg n) time.
• And at most two rotations occur overall.

Thus, insertion into a red-black tree takes O(lg n) time.

Removing a node from a red-black tree

The remove method in RBTree is based on the remove method from the BST class. It calls an overridden version of transplant, which always assigns to v.parent, even if v is the sentinel. By changing the transplant method from a method of BST or RBTree to a method of the appropriate Node inner class, I get dynamic binding: when transplant is called on an RBTree.Node, the appropriate version of transplant runs.

The remove method in RBTree has the following differences from the remove method in BST:

• y is the node either removed from the tree (when z has fewer than two children) or moved within the tree (when z has two children).
• We need to save y's original color to test it at the end, because if it's black, then removing or moving y could cause red-black properties to be violated.
• x is the node that moves into y's original position. It's either y's only child, or the sentinel if y has no children.

• It sets x.parent to point to the original position of y's parent, even if x is the sentinel. x.parent is set in one of two ways:

  • If z is not y's original parent, then x.parent is set in the last line of transplant.
  • If z is y's original parent, then y will move up to take z's position in the tree. The assignment x.parent = y makes x.parent point to the original position of y's parent, even if x is the sentinel.

• If y's original color was black, the changes to the tree structure might cause red-black properties to be violated, and we call rbRemoveFixup at the end to resolve the violations.

If y was originally black, what violations of red-black properties could arise?

1. No violation.

2. If y is the root and x is red, then the root has become red.
3. No violation.
4. Violation if x.parent and x are both red.

5. Any simple path containing y now has one fewer black node.

   • Correct by giving x an "extra black."
   • Add 1 to the count of black nodes on paths containing x.
   • Now property 5 is OK, but property 1 is not.
   • x is either doubly black (if x.isBlack is true) or red & black (if x.isBlack is false).
   • The extra blackness on a node is by virtue of x pointing to the node.

We remove the violations by calling rbRemoveFixup. The idea is to move the extra black up the tree until

• x points to a red & black node, and we turn it into a black node,
• x points to the root, and we just remove the extra black, or
• we can do certain rotations and recolorings and finish.

Within the while-loop of rbRemoveFixup:

• x always points to a nonroot doubly black node.
• w is x's sibling.
• w cannot be the sentinel, since that would violate property 5 at x.parent.

There are eight cases, four of which are symmetric to the other four. As with rbInsertFixup, the cases are not mutually exclusive. We'll look at the cases in which x is a left child.

• Case 1: w is red.

  
  
  
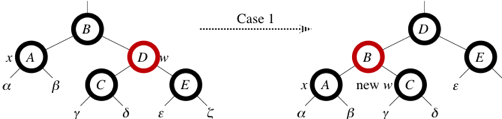
  • w must have black children.
  • Make w black and x.parent red.
  • The left rotate on x.parent.
  • The new sibling of x was a child of w before rotation, and so it must be black.

  • We go immediately into case 2, 3, or 4.

• Case 2: w is black and both of w's children are black.

  
  
  The node with the gray outline is of unknown color c.

  • Take one black off from x (making x singly black) and off w (making w red).
  • Move that black to x.parent.
  • Do the next iteration with x.parent as the new x.
  • If we entered this case from case 1, then x.parent was red, and so the new x is red & black. Then because x.isBlack becomes false, the loop terminates. Then the new x is made black in the last line.

• Case 3: w is black, w's left child is red, and w's right child is black.

  
  
  
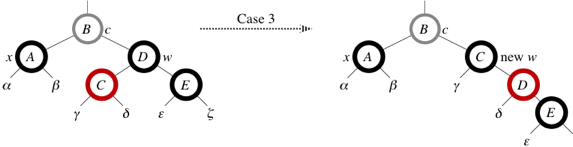
  • Make w red and w's left child black.
  • Then right rotate on w.
  • The new sibling w of x is black with a red right child, and we go immediately into case 4.

• Case 4: w is black, w's left child is black, and w's right child is red.

  
  
  Now there are two nodes of unknown colors, denoted by c and cʹ.

  • Make w be x.parent's color (c).
  • Make x.parent black and w's right child black.
  • Then left rotate on x.parent.
  • Remove the extra black on x, so that x is now singly black, without violating any red-black properties.

  • We are all done! Setting x to the root causes the loop to terminate.

Analysis

It takes O(lg n) time to get through remove up to the call of rbRemoveFixup.

Within rbRemoveFixup:

• Case 2 is the only case in which more iterations occur.

  • x moves up one level.
  • Hence, O(lg n) iterations.
• Each of cases 1, 3, and 4 has one rotation, and so there are at most three rotations in all.

• Hence, O(lg n) time.

Testing

Use the code in RBTreeTest.java to test the RBTree class.