Integrating Clipped Spherical Harmonics
Laurent Belcour - Guofu Xie
University of Montreal
University of Montreal
Christophe Hery - Mark Meyer
Pixar Animation Studio
Pixar Animation Studio
Wojciech Jarosz
Dartmouth College
Dartmouth College
Derek Nowrouzezahrai
McGill University
McGill University

Motivation
- Spherical Integrals are common in rendering
- Shading on surfaces
- Shading in volumes
- Importance sampling
- ...
- Analytical forms are not common
- But are needed by real-time rendering
Motivation: BRDF Integration
- (Quasi) Monte-Carlo
- Approximative (contains error)
- Large number of samples
- Real-Time Rendering
- Sampling is out of the question
- Needs efficiency, allows approximate
- Analytical solutions are welcome
- Must include the light (spherical domain)

BRDF
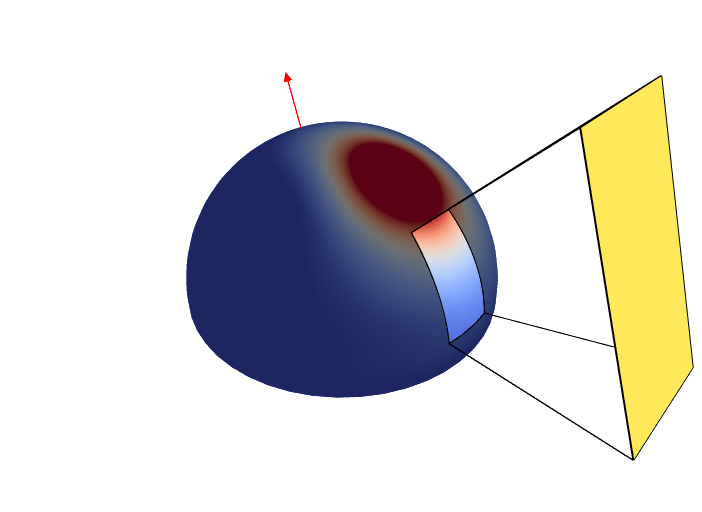
light
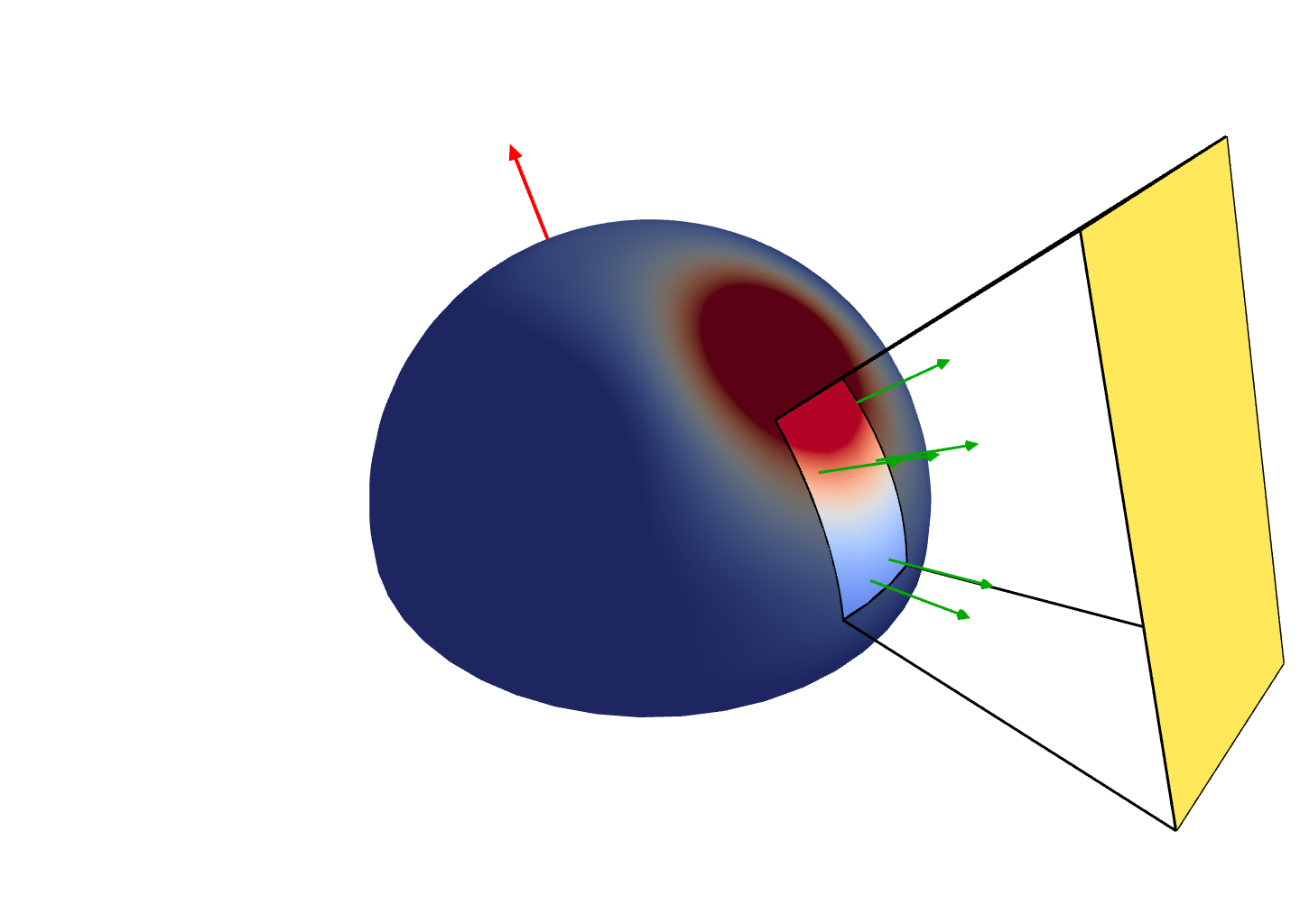
A Few Existing Methods
- But restricted to specific spherical functions
Our Solution
- Integrate Spherical Harmonics expansions on spherical polygons
- Efficient algorithm
- scales well with higher order SH
- We incorporate such analytical solution
- for shading on surfaces
- for shading in volumes
- "What about shadowing/bias ?"
- using control variates
- or a ratio estimator [Heitz et al. 2018]
Inspiration: Axial Moments
- Function of the dot product, $f(\omega) = \langle \omega \cdot \color{red}{\omega_i} \rangle^\color{green}{n}$
- Recursive integration [Arvo 1995]
- Linear with respect to the power $\color{green}{n}$
- Each step integrate another power cosine
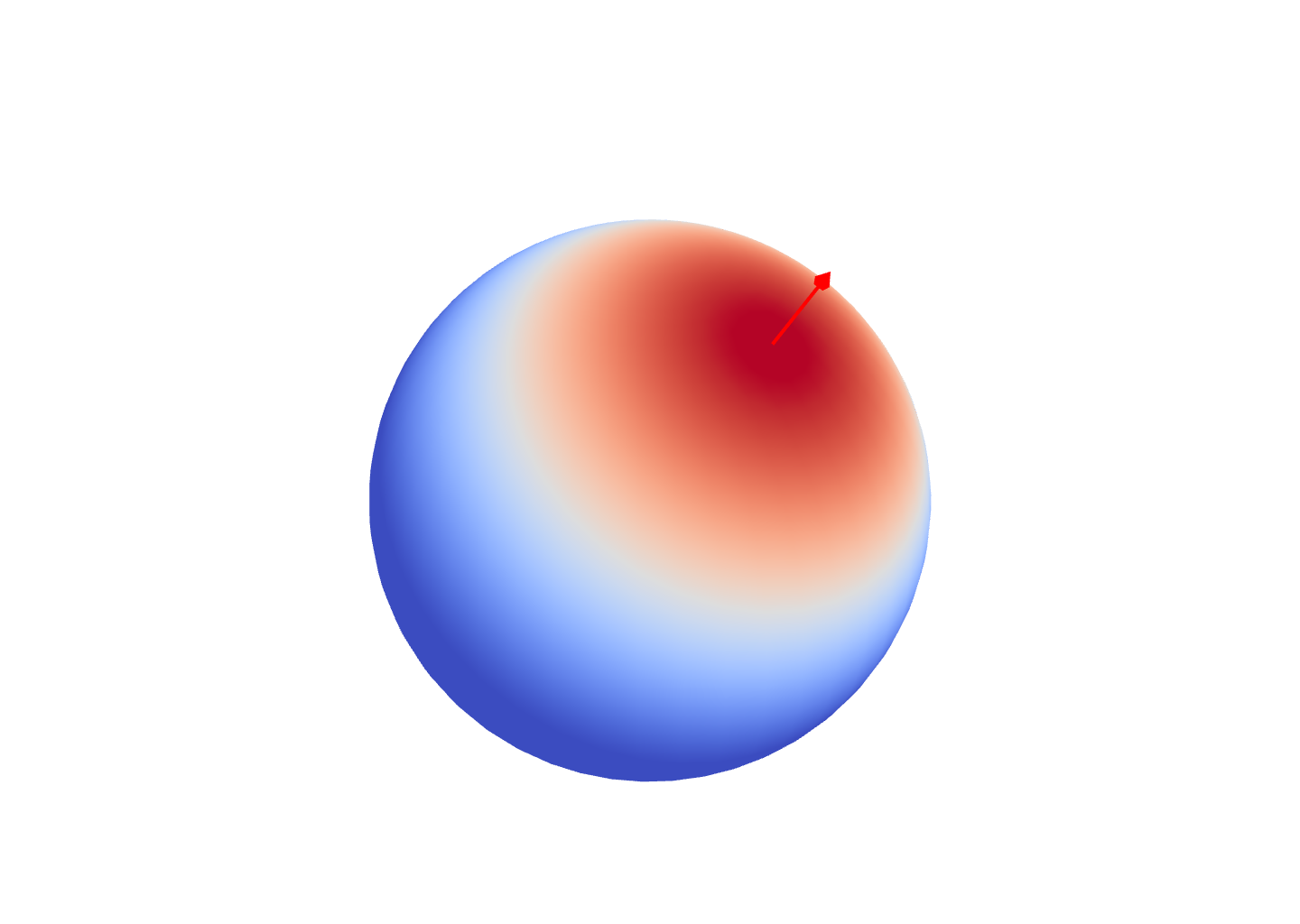
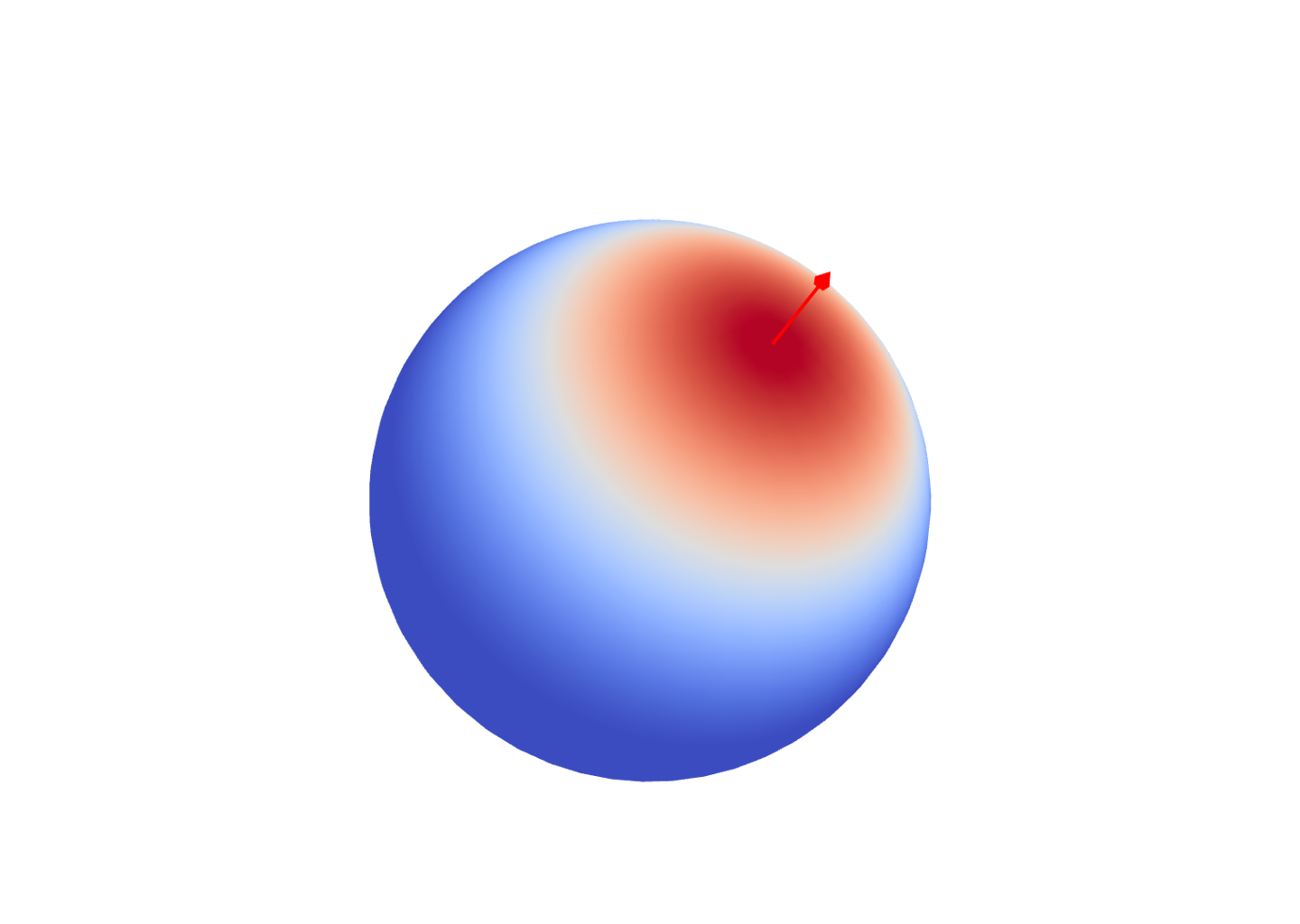

$\color{red}{\omega_i}$
$\langle \omega \cdot \color{red}{\omega_i} \rangle^\color{green}{3}$
$\langle \omega \cdot \color{red}{\omega_i} \rangle^\color{green}{5}$
Outline of Our Method
$$ \int_\mathcal{P} f(\boldsymbol\omega) \mbox{d}\boldsymbol\omega $$
$$ \sum f_{l,m} \int_\mathcal{P} y_{l}^{m}(\boldsymbol\omega) \mbox{d}\boldsymbol\omega $$
$$ \sum c_{k,i} \int_\mathcal{P} \langle \boldsymbol\omega \cdot \boldsymbol\omega_i \rangle^{k} \mbox{d}\boldsymbol\omega $$
lobe sharing
Insight: An Intermediate Step
- Rotated Zonal Harmonics [Nowrouzezahrai et al. 2012]
Decomposing Rotated Zonal Harmonics
That's All Folks!
/* Compute the integral of the SH decomposition with
* `f` coefficients over a spherical polygon `poly`.
*/
function ComputeIntegral(flm, poly) {
// Generate a set of vectors
basis = SharedDirections();
// Compute the conversion matrices
// `A` converts SH to Zonals
// `P` converts Zonals to Axials
A = ZonalWeights(basis);
P = AxialWeights(basis);
AP = A*P;
// Convert the Axial expansion
cpw = flm.transpose() * AP;
// Return the integral using Arvo's method
m = AxialMoments(poly, basis);
return cpw.dot(m);
}
$$
\mathbf{f}^T \mathbf{y} = \sum_{l,m} \mathcal{\color{green}{f_{l,m}}} \left[ \int_{\mathcal{\color{darksalmon}{P}}} y_{l,m}(\omega) \right]
$$
$$
\mathbf{c}^T = \mathbf{f}^T \times AP
$$
$$
\mathbf{f}^T \mathbf{y} = \underbrace{\mathbf{c}^T}_{\mathbf{f}^T \times AP} \times \mathbf{m}
$$
That's All Folks! (How Really?)
- Redudant computation in Arvo's method
- We improve performance by
- sharing axial moment directions
- sharing Arvo's recursive evaluation
- Details are in the paper
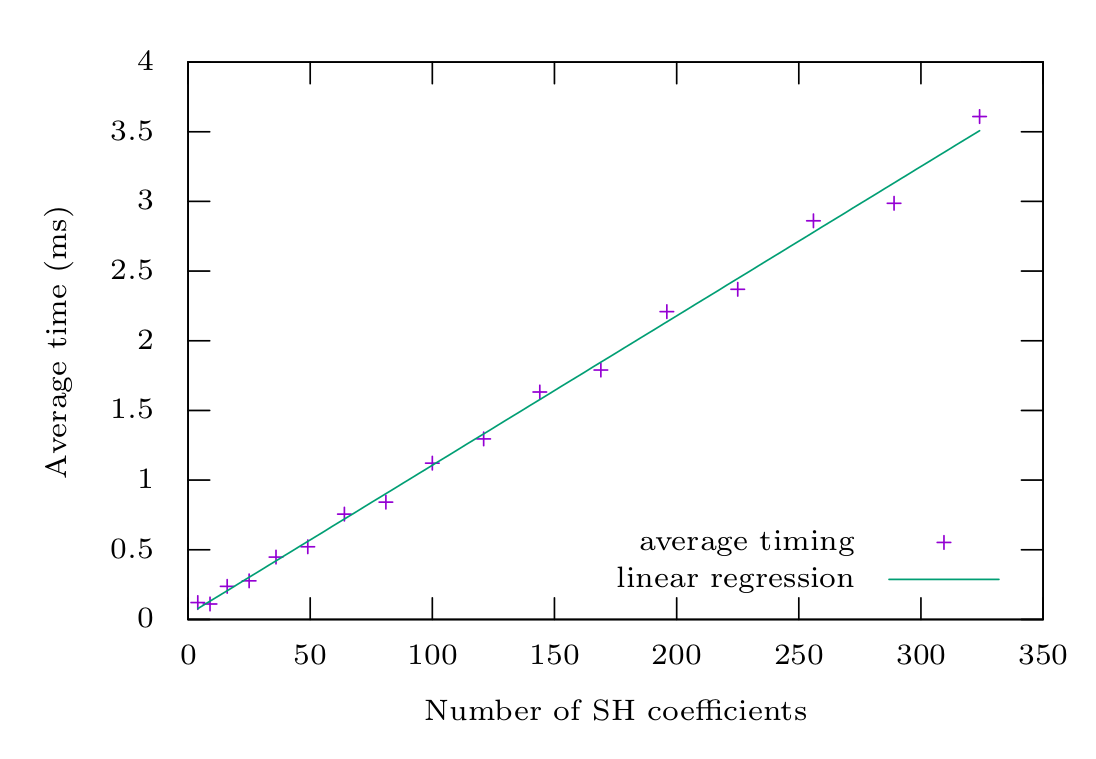
Algorithmic Complexity
- Linear w.r.t. number of SH coefficients
Applications
hierarchichal warping
adding shadows
Surface and Volume Shading

Surface area light

Surface portal light

Volume area light

Volume portal light
Surface Shading: Area Light

Surface area light
$$
\color{green}{\rho(\boldsymbol{\omega}_i, \cdot}) \simeq \mathbf{f} = \mathbf{y}_i^T, \mbox{M} \quad
\mbox{with} \, \, \mathbf{y}_i = y_{l,m}(\boldsymbol{\omega}_i)
$$
[Westin et al. 1992]
Surface Shading: Portal Light

Surface portal light
Volume Shading: Area Light

Volume area light
Volume Shading: Portal Light

Volume portal light
Application: Real-Time Rendering
Application: Control Variates
Our real-time demo lacks shadows
- Analytical solutions have bias
- they do not account for shadows
- they approximate the true BRDF
-
Combine Closed-Form and Monte-Carlo results
$$ I = \color{green}{\int_{\mathcal{P}} y\left(\boldsymbol\omega\right) \mbox{d}\boldsymbol\omega} \, - \, \color{blue}{\sum_{k} \left[ y\left(\boldsymbol\omega_k\right) - f\left(\color{blue}{\boldsymbol\omega_k}\right) \right]} $$
- Visual 'Side effect'
- No noise in unshadowed regions
- Ensure unbiasness w.r.t. $f(\boldsymbol{\omega})$
Application: Control Variates
- Dragon scene
Application: Control Variates
- Fog scene
Application: Control Variates
- San Miguel scene
Summary
- We integrate Spherical Harmonics
- over spherical polygons
- with a closed-form expression
- that is efficient (linear cost)
- We apply this new tool
- to surface and volume shading
- to polygonal portal lights
- to importance sampling
Thank you for your attention
 |
 |
| paper | code |




