15. Network visualization

Graphs | Force-directed layout | Some networks | Programming notes

Graphs

There are many interesting applications where we want to understand relationships among things — social networks (who is friends with whom), biological networks (how are signals carried through the cell), and, yes, even computer networks (how do web pages point to each other). Sometimes the relationships are less explicit, e.g., based on how similar things are to each other (see the Processing exhibition entry the dumpster). There is a lot of work out there on analyzing such data; e.g., see the Visual Complexity site for some nice examples.

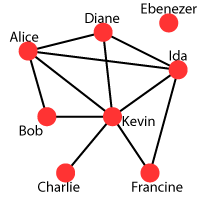
Just as floats and ints represent numbers and booleans true/false values, graphs represent pairwise relationships among things. Processing doesn't have a Graph class built in, so we'll build our own very simple one here. A graph consists of two types of things: vertices (sometimes called nodes) represent the individual objects (e.g., people, proteins, or web pages), and edges represent their relationships (e.g., is friends with, passes a signal to, or links to). Sometimes there's a directionality (e.g., links to vs. is linked from), but we won't worry about that here. When we depict a graph, we typically draw vertices as circles and edges as lines connecting them. In the following example, Alice and Bob are friends, as are Alice and Diane; everybody's friends with Kevin and nobody's friends with poor old Ebenezer.

For the graphs we'll be dealing with, the vertices all have text associated with them. Text is represented in Processing with a type of object called a String. We've actually been using strings for quite some time now, for displaying and printing text. Strings are just arbitrary lists of letters, numbers, etc., enclosed in double quotes, e.g., "Hello, there". We can declare a variable to be of type String, and then assign these values to it, e.g., String msg="hello, there";.

How do we tell Processing what the vertices and edges are for a particular graph? We'll use a file in a special format, and read the file into our program. There are numerous possible file formats; the following sketch uses the core of the Pajek format. In this format, we first have a line that says the number of vertices. We then have one line per vertex, giving it an id number and a label (e.g., the person's name). If a label has spaces, it should be in double quotes. Next is a line that says edges are coming next (although we don't say how many), followed by one line per edge, giving the id numbers of the related vertices. For example:

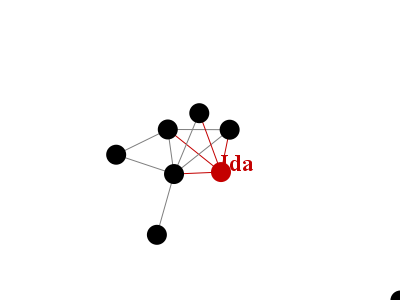
*Vertices 8
1 Alice
2 Bob
3 Charlie
4 Diane
5 Ebenezer
6 Francine
7 Ida
8 Kevin
*Edges
1 2
1 4
1 7
1 8
2 8
3 8
4 7
4 8
6 7
6 8
7 8

The following sketch reads in a file following this format, and fills in a Graph object with Vertex and Edge objects. The details of the reader are a bit hairy; don't worry about them. What's more important is the structure of the objects that have been read in. A graph has an array of vertices and an array of edges. Each vertex just has a label. Each edge simply says which pair of vertices it connects. Here is the data file for this sketch: [friends.txt].

[sketch1]

function setup()
{
  Graph g = new Graph();
  readPajek(g,"friends.txt");
  g.print();
}

function draw() {
}

[applet]

Force-directed layout

Given a bunch of vertices and edges, how can we nicely lay out the graph, as in the friends example above? If we just put the vertices at random positions, they aren't likely to be near their neighbors, and we'll have lines for edges going all over the place. This brings us back to the approach that we saw before that modeled relationships -- springs. Basically, we want to put a spring for each edge, so that neighbors try to be close together. That's not quite enough though, because multiple neighbors of a single vertex (that weren't themselves connected) could try to be in the same place. There's nothing to keep Alice's friends Diane and Bob from overlapping. In addition to springs, we need repulsion (insert your own joke here about repulsion in social networks).

Let's go back to pseudo-physics and come up with a model of repulsion. We dealt before with gravity between a small object and a massive one, which just made the small object accelerate towards the massive one (downward). The underlying gravitational model has each object pull the other towards it (remember that you are indeed pulling the earth towards you just a bit). We'll take that model and just make the objects push away from each other (like aligned magnets, or the same electrical charge). The standard model is F = G*m_i*m_j / d_ij², where G is the gravitational constant, m_i and m_j are the masses of the objects, and d_ij is the distance between the objects.

The following sketch uses our standard old Ball class (with wall-bouncing), and applies repulsion (a negative G) between each pair. Note the nested for-loop to handle each pair just once (1,2 but not 2,1), by starting j at i+1. We ignore masses, so the formula is simplified. We also separate out the component of the force that's applied in the x direction and in the y direction. Some user interface stuff allows a ball to be dragged around (foregoing any other forces).

[sketch2]

Ball[] balls = new Ball[10];
var dragging = -1;  // which ball is being dragged (-1 if none)

var G = 50;  // strength of repulsion

function setup()
{
  createCanvas(400,300);
  smooth();
  noStroke();

  // Start them at random places
  for (var i=0; i<balls.length; i++)
    balls[i] = new Ball(random(width),random(height)); 
}

function draw()
{
  background(0);
  
  // Draw each
  for (var i=0; i<balls.length; i++) {
    if (i == dragging) fill(255,0,0);
    else fill(255);
    balls[i].draw();
  }
  
  // Apply repulsion for each pair
  for (var i=0; i<balls.length; i++) {
    for (var j=i+1; j<balls.length; j++) {
      var dij = dist(balls[i].x,balls[i].y, balls[j].x,balls[j].y);
      if (dij > 0) {
        // Compute repulsive force, and the fraction in each direction
        var f = G/(dij*dij);
        var dx = (balls[j].x-balls[i].x)/dij;
        var dy = (balls[j].y-balls[i].y)/dij;
        // Push each away from the other (unless being dragged)
        if (i != dragging) {
          balls[i].vx -= f*dx;
          balls[i].vy -= f*dy;
        }
        if (j != dragging) {
          balls[j].vx += f*dx;
          balls[j].vy += f*dy;
        }
      }
    }
  }
  // Update velocities and positions
  for (var i=0; i<balls.length; i++) {
    if (i != dragging) balls[i].update();
  }
}

function mousePressed()
{
  // See if beginning to drag
  dragging = -1;
  for (var i=0; i<balls.length; i++)
    if (dist(mouseX,mouseY, balls[i].x,balls[i].y) < balls[i].r)
      dragging = i;
}

function mouseDragged()
{
  // If dragging, update position
  if (dragging >= 0) {
    balls[dragging].x = mouseX;
    balls[dragging].y = mouseY;
  }
}

function mouseReleased()
{
  // Stop dragging and put it at rest (0 velocity)
  if (dragging >= 0) {
    balls[dragging].vx = 0;
    balls[dragging].vy = 0;
    dragging = -1;
  }
}

function keyPressed()
{
  if (key=='G') {  // more repulsion
    G+=10;
    println("G:"+G);
  }
  else if (key=='g') {  // less repulsion
    if (G>10) {
      G-=10;
      println("G:"+G);
    }
  }
  else if (key=='s') {  // stop
    for (var i=0; i<balls.length; i++) {
      balls[i].vx=0; balls[i].vy=0;
    }
  }
  else if (key=='r') {  // reset positions and velocities
    for (var i=0; i<balls.length; i++) {
      balls[i].x = random(width); balls[i].y = random(height);
      balls[i].vx = 0; balls[i].vy = 0;
    }
  }
}

[applet]

We've now got all we need to be able to lay out a graph — springs for edges and repulsions between all vertex pairs. In order to handle larger-scale sets of springs and repulsions, it's necessary to be a bit more careful with how forces are integrated over time. Rather than doing that ourselves, let's turn to a contributed library, Traer physics. Contributed libraries extend Processing various ways. They don't come with Processing and require some (usually straightforward) installation work, described in Ch. 12 of the textbook and in the libraries section of the Processing reference. They also require addition of an appropriate import statement at the top of the sketch.

Following is the previous repulsion sketch rewritten using the Traer physics library. (Note that the library works in 3D, so we keep using 0 for the z value, in positions and velocities.) The models are the same (though the constants somewhat different), but the results end up being better behaved. Overall, it's at a higher level -- we just create particles and repulsions, and ask the physics module to update them. It also gives better results -- notice what happens with our set of particles.

[sketch3]

import traer.physics.*;

Particle[] ps = new Particle[10];
var dragging = -1;  // which particle is being dragged (-1 if none)
var r=10; // uniform radius

ParticleSystem physics;
var G = 1000;  // strength of repulsion


function setup()
{
  createCanvas(400,300);
  smooth();
  noStroke(); 
  
  // Create the physics module, with no inherent gravity and a small amount of drag
  physics = new ParticleSystem(0,0.1);
  
  // Create the particles, with uniform mass of 1, starting at random positions
  for (var i=0; i<ps.length; i++)
    ps[i] = physics.makeParticle(1,random(width),random(height),0);

  // Make them repel each other
  for (var i=0; i<ps.length; i++)
    for (var j=i+1; j<ps.length; j++)
      physics.makeAttraction(ps[i], ps[j], -G, r/2);
}

function draw()
{
  background(0);

  // Draw each
  for (var i=0; i<ps.length; i++) {
    if (i==dragging) fill(255,0,0);
    else fill(255);
    ellipse(ps[i].position().x(), ps[i].position().y(), 2*r,2*r);
  }
  
  // Update    
  physics.tick();
  for (var i=0; i<ps.length; i++)
    handleBoundaryCollisions(ps[i]);
}

// Bounce off the wall (and lose a little velocity)
// From an example at the traer.physics site
function handleBoundaryCollisions(Particle p)
{
  if (p.position().x() < 0 || p.position().x() > width)
    p.velocity().set(-0.9*p.velocity().x(), p.velocity().y(), 0);
  if (p.position().y() < 0 || p.position().y() > height)
    p.velocity().set(p.velocity().x(), -0.9*p.velocity().y(), 0);
  p.position().set(constrain(p.position().x(), 0, width), constrain(p.position().y(), 0, height), 0); 
}

function mousePressed()
{
  // See if beginning to drag
  dragging = -1;
  for (var i=0; i<ps.length; i++) {
    if (dist(mouseX,mouseY, ps[i].position().x(),ps[i].position().y()) < r)
      dragging = i;
  }
  if (dragging >= 0) ps[dragging].makeFixed();
}

function mouseDragged()
{
  // If dragging, update position
  if (dragging >= 0)
    ps[dragging].position().set(mouseX,mouseY,0);
}

function mouseReleased()
{
  // Stop dragging and put it at rest (0 velocity)
  if (dragging >= 0) {
    ps[dragging].makeFree();
    ps[dragging].velocity().set(0,0,0);
    dragging = -1;
  }
}

function keyPressed()
{
  if (key=='G') {  // more repulsion
    G+=100;
    println("G:"+G);
  }
  else if (key=='g') {  // less repulsion
    if (G>100) {
      G-=100;
      println("G:"+G);
    }
  }
  else if (key=='s') {  // stop
    for (var i=0; i<ps.length; i++)
      ps[i].velocity().set(0,0,0);
  }
  else if (key=='r') {  // reset positions and velocities
    for (var i=0; i<ps.length; i++) {
      ps[i].position().set(random(width),random(height),0);
      ps[i].velocity().set(0,0,0);
    }
  }
}

[applet]

Some networks

Now let's put it all together. In the following sketch, Graph has a method model() that generates the springs and repulsions. Each vertex has a particle; the physics module updates the particle and thereby moves the vertex. (When the vertex wants to draw itself, it asks the particle where.)

[sketch4]

import traer.physics.*;

ParticleSystem physics;
var G = 1000;     // strength of repulsion
var k = 0.05;   // spring constant
var damp = 0.1; // spring damping
var rest = 50;  // spring rest length

Graph g;

function setup()
{
  createCanvas(400,300);
  smooth();
  noStroke(); 
  textFont(loadFont("David-Bold-24.vlw"));
  
  physics = new ParticleSystem(0,0.1);

  g = new Graph();
  readPajek(g,"friends.txt");
  g.model(physics,G,k,damp,rest);
}

function draw()
{
  // Display
  background(255);
  g.mouseOver();
  g.draw();

  // Update  
  physics.tick();
  g.update();
}

function mousePressed()
{
  g.pressed();
}

function mouseDragged()
{
  g.dragged();
}

[Graph]

class Vertex {
  String label;
  Particle p;    // for the motion of this vertex
  var r=10;      // radius
  var isLocked=false;  // not moving
  var showLabel=false, showLabelOnce=false;
  
  Vertex(String label)
  {
    this.label = label;
  }

  function draw()
  {
    if (isLocked) fill(196,0,0);
    else fill(0);
    ellipse(p.position().x(), p.position().y(), 2*r,2*r);
  }
  
  function label()
  {
    if (isLocked || showLabel || showLabelOnce) {
      if (isLocked) fill(196,0,0);
      else fill(0,196,0);
      text(label, p.position().x(), p.position().y());
      showLabelOnce = false;
    }
  }

  function update()
  {
    // Bounce off the wall (and lose a little velocity)
    // From an example at the traer.physics site
    if (p.position().x() < 0 || p.position().x() > width)
      p.velocity().set(-0.9*p.velocity().x(), p.velocity().y(), 0);
    if (p.position().y() < 0 || p.position().y() > height)
      p.velocity().set(p.velocity().x(), -0.9*p.velocity().y(), 0);
    p.position().set(constrain(p.position().x(), 0, width), constrain(p.position().y(), 0, height), 0); 
  }
}

class Edge {
  Vertex a, b;

  Edge(Vertex a, Vertex b)
  {
    this.a = a; 
    this.b = b; 
  }
  
  function draw()
  {
    if (a.isLocked || b.isLocked) stroke(196,0,0);
    else stroke(128);
    line(a.p.position().x(), a.p.position().y(),
         b.p.position().x(), b.p.position().y());
  }
}

class Graph {
  Vertex[] vertices;
  Edge[] edges;
  var locked = -1;  // which vertex is being dragged (-1 if none)

  function model(ParticleSystem physics, var G, var k, var damp, var rest)
  {
    // Create the particles
    for (var i=0; i<vertices.length; i++)
      vertices[i].p = physics.makeParticle(1,random(width),random(height),0);

    // Make them repel each other
    for (var i=0; i<vertices.length; i++)
      for (var j=i+1; j<vertices.length; j++)
        physics.makeAttraction(vertices[i].p, vertices[j].p, -G, 0.25*(vertices[i].r+vertices[j].r));

    // Springs for edges
    for (var i=0; i<edges.length; i++)
      physics.makeSpring(edges[i].a.p, edges[i].b.p, k, damp, rest); 
  }  

  function draw()
  {
    // Edges
    for (var i=0; i<edges.length; i++) edges[i].draw();

    // Vertices
    noStroke();
    for (var i=0; i<vertices.length; i++) vertices[i].draw();
    
    // Labels
    for (var i=0; i<vertices.length; i++) vertices[i].label();
  }

  function update()
  {
    for (var i=0; i<vertices.length; i++)
      vertices[i].update();
  }

  function pressed()
  {  
    var grabbed = overVertex();
    if (locked >= 0 && mouseButton == LEFT) {
      // unlock existing lock
      vertices[locked].isLocked = false;
      vertices[locked].p.makeFree();
      vertices[locked].p.velocity().set(0,0,0);
      locked = -1;
    }
    
    if (grabbed >= 0) {
      if (mouseButton == LEFT) {
        // new lock
        locked = grabbed;
        vertices[locked].isLocked = true;
        vertices[locked].p.makeFixed();
      }
      else if (mouseButton == RIGHT) {
        // toggle label
        vertices[grabbed].showLabel = !vertices[grabbed].showLabel;
      }
    }
  }

  function dragged()
  {
    if (locked >= 0)
      vertices[locked].p.position().set(mouseX,mouseY,0);
  }

  function mouseOver()
  {
    var over = overVertex();
    if (over >= 0) vertices[over].showLabelOnce = true;
  }
  
  // Returns index of vertex which the mouse is over, or -1 if none
  var overVertex()
  {
    var over=-1;
    for (var i=0; i<vertices.length; i++)
      if (dist(mouseX,mouseY, vertices[i].p.position().x(),vertices[i].p.position().y())
          < vertices[i].r)
        over = i;
    return over;
  }
}

[applet]

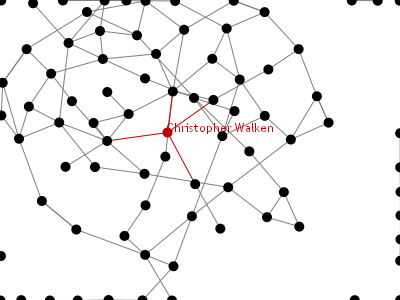
We can do this on larger networks, although not too large. One example of a social network is actors who have been in movies together (the Kevin Bacon game). There's a (slightly out of date now) dataset of some movies and actors, and which actors were in which movies. This dataset is too large for our system. The following sketch restricts the movies by date (say, from 2001 on) and the actors by number of roles they've had in those movies (say, at least 4). That gives us something a bit more manageable. It's still kind of hard to make sense of, but gives a feel for a more complex social network.

The basic graph code is the same, except that now edges have labels too (the movies in which the actors played). There is a special-purpose function to read in the movie data; somewhat hairy, but not the focus of what we're doing here, so treat it as a black box if you like. Here is the data: [movies.txt], [actors.txt], [movie_actors.txt].

[sketch5]

import traer.physics.*;

ParticleSystem physics;
var G = 1000;     // strength of repulsion
var k = 0.1;   // spring constant
var damp = 0.1; // spring damping
var rest = 20;  // spring rest length

Graph g;

function setup()
{
  createCanvas(400,300);
  smooth();
  noStroke(); 
  textFont(loadFont("TrebuchetMS-12.vlw"));
  
  physics = new ParticleSystem(0,0.5);

  g = new Graph();
  readMovies(g,2001,4);
  g.model(physics,G,k,damp,rest);
}

function draw()
{
  background(255);
  g.mouseOver();
  g.draw();
  
  physics.tick();
  g.update();
}

function mousePressed()
{
  g.pressed();
}

function mouseDragged()
{
  g.dragged();
}

[applet]

Programming notes

String: String is another built-in data type (like int, float, and boolean). It holds text. String values are given in double quotes, e.g., "Hello". Strings can be parameters to functions, e.g., that's what println() wants. There are various functions and operators for manipulating strings; see the Processing reference (extended) for a list. We've already used the plus sign to concatenate two strings together, for printing.
import: Some functionality provided in Processing, or provided as an extension to Processing, is only available if a library is imported. The menu Sketch | Import Library adds an appropriate statement at the top of the sketch, or you can do it by hand. Processing libraries can immediately be imported, while contributed libraries require installation first. See the library reference.